Sähkötekniikan teoreettiset perusteet: Nodal Stress Method

Solmun jännitysten menetelmä on laskelmasähköiset piirit, joissa muuttujat ovat ketjujen solmujen jännitysten arvoja suhteessa perussolmuun. Yhtälöt kootaan ensimmäisen Kirchhoff-lain perusteella, jonka avulla voimme vähentää järjestelmän yhtälöiden lukumäärää arvoon k-1, missä k on ketjun solmujen lukumäärä. Tätä menetelmää käytetään parhaiten, kun sähköpiirin haarojen lukumäärä on suurempi kuin kaksi. Solmun jännitystekniikka on löytänyt sovelluksen sähköpiirien tietokoneiden simulointiohjelmissa, johtuen algoritmin yksinkertaisuudesta solmuyhtälöiden muodostamiseksi.

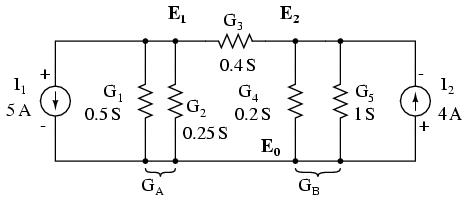
Nodal stressit ovat jännitteitä mielivaltaisen vertailusolmun (jossa potentiaalin oletetaan olevan nolla) ja kunkin solmun välillä. Kaavioissa vertailusolmu näytetään maadoitettuna.

Tarkastellaan erilaisia ​​menetelmiä sähkövirtapiirien laskemiseksi

Tämän menetelmän ydin on ratkaistayhtälöjärjestelmät, joiden avulla kunkin piirin solmun potentiaalit määritetään suhteessa vertailusolmuun. Tämän jälkeen piirit lasketaan Ohmin lain mukaan, eli määritetään kaikkien haarojen virtojen arvot.

Monimutkaisten ketjujen laskeminen suoritetaan seuraavassa sekvenssissä:

1. Kaavamainen kaavio laaditaan, kaikki elementit.

2. Määritetään mielivaltainen vertailusolmu. Ja on suositeltavaa valita tällainen solmu, jossa suurin osa haaroista lähenee.

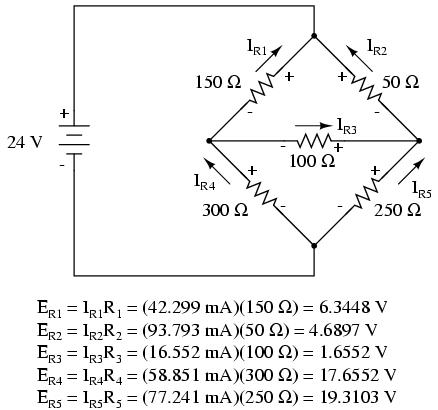
3. Kaaviossa on esitetty mielivaltainen virtaussuunta kaikilla haaroilla, mikä näkyy kaaviossa.

4. Jäljellä olevien solmujen potentiaalien laskemiseksi valitun vertailusolmun suhteen kootaan yhtälöjärjestelmä.

Tällaisen järjestelmän yhtäläisyyksillä on seuraava muoto:

U1G11 - U2G12 - ... - UsG1s - UnG1n = Σ1EG + Σ1J

-U1G21 + U2G22 - ... - UsG2s - UnG2n = Σ2EG + Σ2J

........................................................................................

U1Gn1 - U2Gn2 - ... - UsGns + UnGnn = ΣnEG + ΣnJ, jossa:

• G on solmuun liittyvien oksojen johtokyvyn summa;
• U - solmujännitteiden arvo;
• ΣEG on tuotteiden arvojen algebrallinen summaEMF-oksat, jotka ovat solmun vieressä, niiden johtavuudesta. (Siinä tapauksessa, että sähkömotorinen voima toimii kokoonpanon suuntaan, kun tuote annetaan "+" merkki päinvastaisessa tapauksessa - "-").

Yllä kuvattu yhtälöjärjestelmä ratkaisee helpostilaskea tarvittavat arvot solmun jännitteet. Hänellä on nimi - järjestelmän solmukohtien yhtälöt. Tapauksessa, jossa monimutkainen sähköinen piiri koostuu n: nnen solmujen määrä on tarpeen, jotta solmukohtien yhtälö on yksi vähemmän kuin solmujen lukumäärä. Koska kaikki yhtälöt on kirjoitettu perusteella Kirchhoffin ensimmäinen laki, lasketun ketju olisi koskettava yksinomaan riippumattomista lähteistä sähkövirran. Tapauksessa, jossa piiri käsittää jännitelähteen, on korvattava yhtä virtalähteiden. Lisäksi solmukohtien yhtälö voidaan kirjoittaa matriisimuodossa.

5. Kaavojen järjestelmä ratkaistaan ​​suhteessa solmun jännityksiin, määrittäen niiden arvot.

6. Tämän jälkeen kullekin haaralle kaikki virtapiirin sähkövirran arvot lasketaan erikseen Ohmin lain mukaan.

I = (Ua - Ub + ΣEab) / ΣRab, missä:

• I on haaravirran arvo;
• Ua on solmun a potentiaali;
• Ub on solmun b potentiaali;
• ΣEab on tietyn haaran algebrallinen summa;
• ΣRab - aritmeettinen summa vastus haara.

Solmun jännitystekniikka kahdelle solmulle muodostuvista piireistä

Laskettaessa sähköpiirejä, jotka sisältävät vain kaksi solmua, yhtälöjärjestelmä koostuu yhdestä yhtälöstä, josta on mahdollista suoraan laskea solmujännitteen arvo:

U = (ΣnEnGn + ΣnJn) / ΣmGm, missä:

• ΣnEnGn on haarojen emf-tuotteiden arvojen algebrallinen summa näiden oksojen johtavuudessa;
• ΣnJn on nykyisten lähteiden algebrallinen summa;
• ΣmGm on kaikkien solmujen välisten haarojen johtavuuksien aritmeettinen summa.

Solmun rasitusmenetelmällä on seuraavat matemaattiset edut: laskujen helppous ja aritmeettisten operaatioiden määrän huomattava väheneminen.

</ p>