Kvadraattisten yhtälöiden ratkaiseminen ja graafien rakentaminen

Kvadraattiset yhtälöt ovat toisten yhtäläisyyksiätasolla yhden muuttujan kanssa. Ne heijastavat parabolan käyttäytymistä koordinaattitasolla. Vaaditut juuret edustavat pisteitä, joilla kaavio leikkaa OX-akselin. Kertoimilla voidaan ensin tietää tietyt parabola-ominaisuudet. Esimerkiksi, jos numero on arvo x ennen², negatiivinen, sitten parabolan oksat etsivät. Lisäksi on olemassa useita temppuja, joiden avulla voit huomattavasti yksinkertaistaa tietyn yhtälön ratkaisua.

Neliöllisten yhtälöiden tyypit

Koulussa opetetaan useita erilaisia ​​neliöitäyhtälöt. Riippuen tästä, niiden ratkaisujen menetelmät ovat myös erilaiset. Erikoistyypeistä voidaan erottaa neliölliset yhtälöt parametrilla. Tämä tyyppi sisältää useita muuttujia:

ah²+ 12x-3 = 0

Seuraava variaatio on yhtälö, jossa muuttujaa ei ole yksittäinen luku vaan koko ilmentymä:

21 (x + 13)²-17 (x + 13) -12 = 0

On syytä harkita, että tämä on yleinen käsitysneliö yhtälöt. Joskus ne esitetään muodossa, jossa ne täytyy ensin järjestää, moninkertaistaa tai yksinkertaistaa.

4 (x + 26)²- (- 43x + 27) (7-x) = 4x

Ratkaisun periaate

Kvadraattiset yhtälöt ratkaistaan ​​seuraavalla tavalla:

1. Tarvittaessa on hyväksyttävien arvojen alue.
2. Kaava lasketaan vastaavaan muotoon.
3. Vastaava kaava on erottava: A = b²-4as.
4. Erottuvan arvon mukaan tehdään tehtävästä johtopäätöksiä. Jos A> 0, sanomme, että yhtälöllä on kaksi erillistä juuria (A: lle).
5. Tämän jälkeen löydetään yhtälön juuret.
6. Lisäksi (tehtävästä riippuen) piirrataan kaavio tai arvo löytyy tietystä pisteestä.

Neliarvoiset yhtälöt: Vieta-lause ja muut muutokset

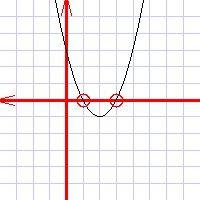
Jokainen koululainen haluaa vilkuttaa oppiaiheensa tietämyksellään, kekseliäisyydellään ja taidoillaan. Neliöllisten yhtälöiden tutkimuksessa tämä voidaan tehdä usealla eri tavalla.

Siinä tapauksessa, että kerroin a = 1, voimmepuhuu Vietin teoreeman soveltamisesta, jonka mukaan juurien summa on yhtä suuri kuin b: n arvo, joka on x: n edessä (nykyisen kanssa vastakkaisella merkillä) ja tuotteen x₁ ja x₂ rinnastetaan. Tällaisia ​​yhtälöitä kutsutaan pienemmiksi.

x²-20x + 91 = 0,

x_{1 *}x₂= 91 ja x₁+ x₂= 20, => x₁= 13 ja x₂= 7

Toinen tapa yksinkertaisesti yksinkertaistaa matemaattista työtä on käyttää parametrien ominaisuuksia. Joten, jos kaikkien parametrien summa on 0, niin saamme x: n₁= 1 ja x₂= c / a.

17x²-7x-10 = 0

17-7-10 = 0, siis juuri 1: x₁= 1, ja juuri z: x₂= -10 / 12

Jos kertoimien a ja c summa on b, niin x₁= -1 ja vastaavasti x₂= -c / a

25x²+ 49x + 24 = 0

25 + 24 = 49, siis x₁= -1 ja x₂= -24 / 25

Tämä lähestymistapa kvadraattisten yhtälöiden ratkaisemiseenyksinkertaistaa huomattavasti laskentaprosessia ja säästää myös valtavasti aikaa. Kaikki toimenpiteet voidaan toteuttaa mielessä ilman, että kulutetaan arvokasta minuuttia valvontaa tai tarkistustyötä kerrottuna sarakkeessa tai käyttämällä laskinta.

Neliarvoiset yhtälöt toimivat linkkinänumeroiden ja koordinaattitason välillä. Jos haluat nopeasti ja helposti muodostaa parabolan vastaavan funktion, sen vertailun löytämisen jälkeen on tarpeen vetää pystysuora viiva kohtisuoraan x-akseliin nähden. Tämän jälkeen jokainen saatu piste voidaan peilata tietyn viivan suhteen, jota kutsutaan symmetrian akseliksi.

</ p>